Analyse des Systèmes de Premier Ordre

Les systèmes de premier ordre sont parmi les modèles les plus simples mais aussi les plus répandus en automatique. Ils permettent de décrire le comportement dynamique de nombreux procédés physiques : circuits RC, systèmes thermiques, capteurs, etc. Ce chapitre introduit leurs caractéristiques temporelles et fréquentielles, et montre comment les relier aux paramètres physiques du système.

Modélisation d'un système passe-bas (LP)

Equation Différentielle

Un système LTI peut être décrit par une équation différentielle liant l'entrée $x(t)$ et la sortie $y(t)$. Pour les systèmes passe-bas d'ordre 1, cette équation différentielle est donnée par:

$$\tau \frac{dy(t)}{dt}+y(t)=Kx(t)$$

• $K$ : gain statique,
• $\tau$ : constante de temps (s).

Fonction de Transfert

Pour faciliter l'analyse des systèmes LTI, il est courant de recourir à la notion de fonction de transfert. La fonction de transfert d'un système Passe-bas (LP) d'ordre 1 est donnée par:

$$H(s)=\frac{Y(s)}{X(s)}=\frac{K}{\tau s+1}$$

Pôles et Zéros

Un système Passe-bas (LP) d'ordre 1 possède :

• un unique pôle négatif en $s=-\frac{1}{\tau }$,
• aucun zéro.

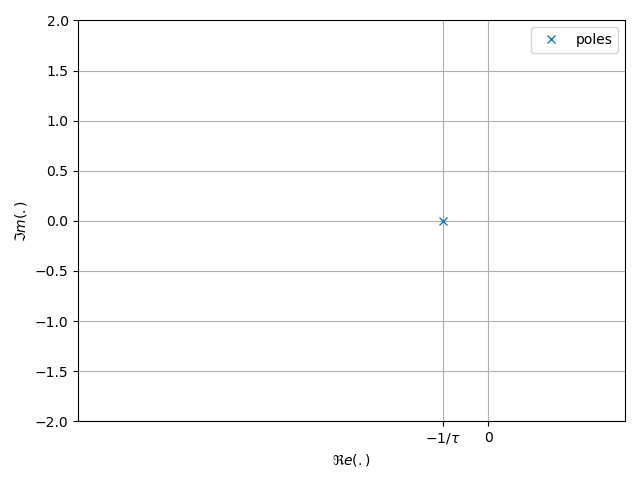
La figure suivante présente le diagramme des pôles et des zéros d'un filtre passe-bas de premier ordre. Ce système possède un unique pôle situé sur l'axe des réels. Lorsque $\tau >0$, ce pôle est strictement négatif et le système est stable.

Diagramme des pôles et des zéros d'un premier ordre LP

Réponse Temporelle

Cette section montre comment obtenir la sortie du système pour différents signaux en entrée.

Réponse Impulsionnelle

La réponse impulsionnelle correspond à la réponse du système lorsque l'entrée est une impulsion de Dirac d'amplitude $E$ ($x(t)=E\delta (t)$). Pour un système LP d'ordre 1, la réponse impulsionnelle est donnée par :

$$y(t)=\frac{KE}{\tau }{e}^{-\frac{t}{\tau }}u(t)$$

Démonstration

Dans le domaine de Laplace, une impulsion de Dirac d'amplitude $E$ est représentée par une constante $X(s)=E$. La sortie $Y(s)$ est alors donnée par :

$$Y(s)=H(s)X(s)=\frac{K}{\tau s+1}\cdot E$$

On obtient donc :

$$Y(s)=\frac{KE}{\tau s+1}=\frac{KE}{\tau }\frac{1}{s+\frac{1}{\tau }}$$

En utilisant la transformée inverse de Laplace, on reconnaît que la fonction suivante dans le domaine temporel :

$${\mathcal{L}}^{-1}\left(\frac{1}{s+\frac{1}{\tau }}\right)=e^{-\frac{t}{\tau }}u(t)$$

Ainsi, on obtient directement :

$$y(t)=\frac{KE}{\tau }{e}^{-\frac{t}{\tau }}u(t)$$

où $u(t)$ est la fonction échelon.

Exemple

La figure suivante présente la réponse impulsionnelle d'un filtre passe-bas de premier ordre lorsque l'entrée est une impulsion d'amplitude $E$.

Réponse impulsionnelle d'un premier ordre LP

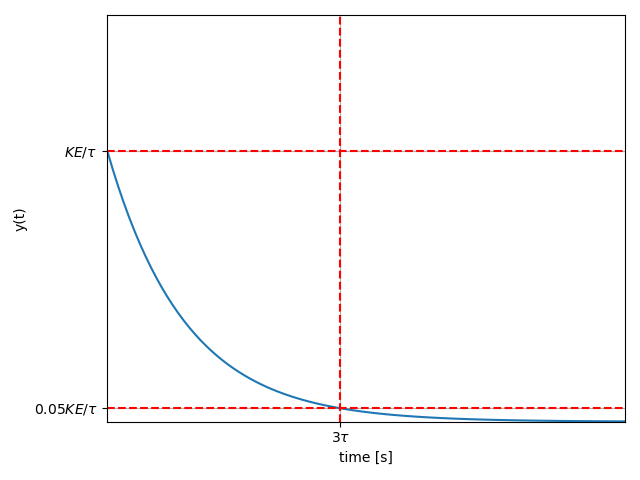
Il est possible d'établir que la réponse impulsionnelle présente les propriétés suivantes:

• Valeur initiale: $y(0^{+})=\frac{KE}{\tau }$,
• Valeur finale: $y(\mathrm{\infty })=0$,
• Valeur en $t_r=3\tau$, $y(3t_r)\approx 0.05\frac{KE}{\tau }$.

Réponse Indicielle

La réponse indicielle correspond à la réponse du système lorsque l'entrée est un échelon d'amplitude $E$ ($x(t)=Eu(t)$). Pour un système LP d'ordre 1, la réponse indicielle est donnée par :

$$y(t)=KE(1-e^{-\frac{1}{\tau }t})u(t)$$

Démonstration

Dans le domaine de Laplace, la sortie s'exprime sous la forme :

$$Y(s)=H(s)X(s)=\frac{KE}{s(\tau s+1)}$$

En utilisant une décomposition en éléments simples, nous obtenons :

$$Y(s)=\frac{KE}{s(\tau s+1)}=\frac{c_1}{s}+\frac{c_2}{\tau s+1}$$

La constante $c_1$ s'obtient en multipliant $Y(s)$ par $s$ et en posant $s=0$:

$$c_1={sY(s)|}_{s=0}=\frac{KE}{\tau s+1}=KE$$

La constante $c_2$ s'obtient en multipliant $Y(s)$ par $\tau s+1$ et en posant $s=-1/\tau$:

$$c_2={(\tau s+1)Y(s)|}_{s=-1/\tau }={\frac{KE}{s}|}_{s=-1/\tau }=-KE\tau$$

Ainsi, $Y(s)$ peut être écrit comme :

$$Y(s)=\frac{KE}{s}-\frac{KE\tau }{\tau s+1}$$

En utilisant la transformée de Laplace inverse, nous obtenons finalement :

$$y(t)=KEu(t)-KE{e}^{-\frac{t}{\tau }}u(t)=KE(1-e^{-\frac{t}{\tau }})u(t)$$

Exemple

La figure suivante présente l'allure de la réponse indicielle lorsque l'entrée est un échelon d'amplitude $E$.

Réponse indicielle d'un premier ordre LP

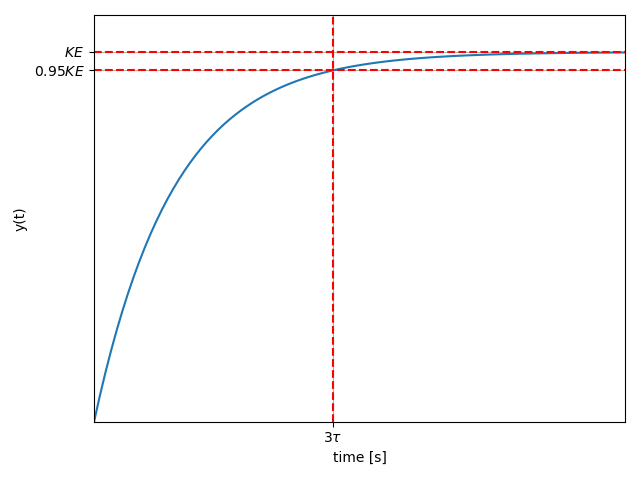
La réponse indicielle suit une exponentielle croissante et se stabilise vers une valeur finie. Il est possible de démontrer les propriétés suivantes:

• Valeur initiale : $y(0)=0$,
• Valeur finale : $y(\mathrm{\infty })=KE$,
• Temps de réponse à $\pm 5\mathrm{\%}$ : $y(t_r)=0.95y(\mathrm{\infty })$ avec $t_r\approx 3\tau$ s,
• Pas de dépassement : $y(\mathrm{\infty })=max(y(t))=KE$.

Temps de réponse

Pour un système de premier ordre, le temps de réponse à $\pm 5$ est égal à $t_r=3\tau$.

Réponse Fréquentielle (Harmonique)

Expression

La réponse fréquentielle d'un système passe-bas (LP) de premier ordre est donnée par :

$$H(j\omega )=\frac{K}{1+j\omega \tau }=\frac{K}{1+j\frac{\omega }{{\omega }_c}}$$

avec ${\omega }_c=\frac{1}{\tau }$. La réponse fréquentielle est une fonction $\mathbb{R}\to \mathbb{C}$. Pour analyser cette réponse, il est courant de recourir aux décompositions suivantes:

• Partie réelle / Partie imaginaire: $H(j\omega )=\mathrm{\Re }e(H(j\omega ))+j\mathrm{\Im }m(H(j\omega ))$
• Module / argument: $H(j\omega )=|H(j\omega )|e^{j\arg (H(j\omega ))}$

Module et Argument

Pour un système passe-bas de premier ordre, le module et l'argument de la réponse fréquentielle s'expriment sous la forme:

• Module :

$$|H(j\omega )|=\frac{|K|}{\sqrt{1+(\omega \tau {)}^2}}$$

• Argument:

$$\arg [H(j\omega )]=\arg [K]-\arctan (\omega \tau )$$

Notons que lorsque $K>0$, $\arg [K]=0$.

Diagramme de Bode

Le diagramme de Bode est composé de deux graphiques :

• le premier graphique présente le module $|H(j\omega )|$ (en dB) en fonction $\omega$ sur une échelle logarithmique.
• le second graphique présente l'argument $\arg [H(j\omega )]$ (en deg) en fonction $\omega$ sur une échelle logarithmique.

Les figures suivantes présentent l'allure du module et de l'argument pour un système passe-bas de premier ordre.

Représentation du module

Réponse fréquentielle d'un premier ordre LP: Module

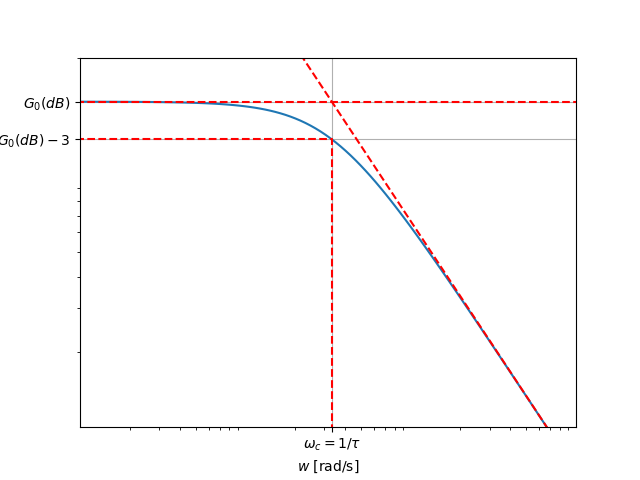
Le module évolue de $G_0(dB)=20{\log }_{10}(|K|)$ (pour $\omega =0$ rad/s) à $-\mathrm{\infty }$ dB (pour $\omega \to \mathrm{\infty }$). En ${\omega }_c=\frac{1}{\tau }$ (rad/s), le module est égal à $|H(j{\omega }_c){|}_{dB}=20{\log }_{10}(|K|)-3$ dB. Pour $\omega \gg {\omega }_c$, le module suit une asymptote égale :

$$\underset{\omega \to \mathrm{\infty }}{lim}|H(j\omega ){|}_{dB}\approx 20{\log }_{10}(|K|)-10{\log }_{10}\left(\frac{\omega }{{\omega }_c}\right)$$

Pulsation de coupure

Pour un système de premier ordre, la pulsation de coupure à $-3dB$ est égale à ${\omega }_c=\frac{1}{\tau }$.

Représentation de l'argument

Réponse fréquentielle d'un premier ordre LP: Argument

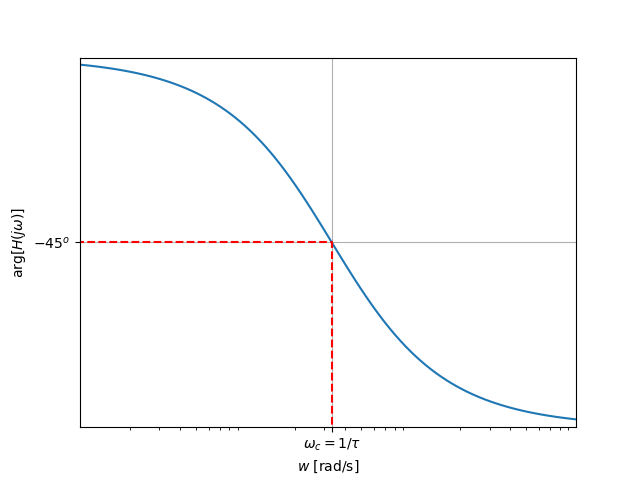
Lorsque $K>0$, l'argument évolue de $0^o$ (pour $\omega =0$ rad/s) à $-{90}^o$ (pour $\omega \to \mathrm{\infty }$). En ${\omega }_c=\frac{1}{\tau }$ (rad/s), l'argument est égal à $\arg [H(j{\omega }_c)]=-{45}^o$. Notons que si $K<0$, la phase est simplement translatée de $180$ degrés.

Diagramme de Black-Nichols

Le diagramme de Black-Nichols est une représentation où l'on trace l'argument $\arg (H(j\omega ))$ en fonction du module $20{\log }_{10}(|H(j\omega )|)$ (en dB).

La figure suivante présente le diagramme de Black-Nichols pour un système passe-bas de premier ordre.

Diagramme de Black Nichols d'un premier ordre LP

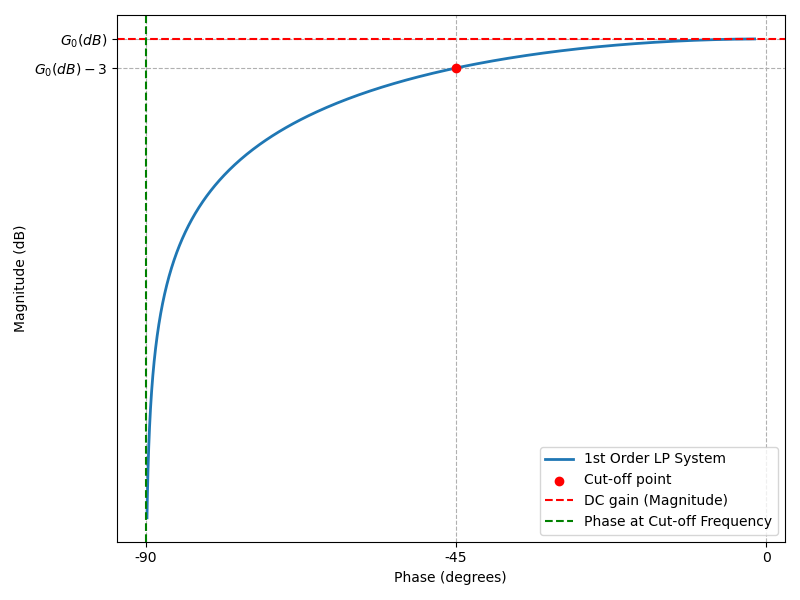
Pour $K>0$, lorsque $\omega$ évolue de $0$ à $\mathrm{\infty }$, la courbe se déplace du point $(20{\log }_{10}(|K|),0^{\circ })$ au point ($-\mathrm{\infty },-{90}^{\circ }$). En ${\omega }_c=\frac{1}{\tau }$, la courbe passe par le point $(20{\log }_{10}(|K|)-3dB,-{45}^{\circ })$.