Stabilité des Systèmes en Boucle Fermée
Objectif
Dans ce chapitre, nous montrons comment analyser la stabilité d'un système en boucle fermée à partir du lieu de Black de la boucle ouverte.
Cadre général: stabilité BIBO
Un système est dit BIBO stable si lorsque son entrée est bornée, sa sortie l'est également. Pour les systèmes continus, un système est BIBO stable si et seulement si sa réponse impulsionnelle est absolument intégrable c-à-d :
Condition sur les pôles
La fonction de transfert d'un système d'ordre
où
Au niveau temporel, chaque pôle
- à une composante du type
pour les pôles réels , - à une composante du type
pour les pôles complexes-conjugués .
Nous constatons alors que, pour qu'un système soit stable, les arguments des termes exponentiels doivent être négatifs. Cette propriété permet de relier directement la notion de stabilité aux pôles du système
Stabilité
Un SLIT continu est BIBO stable si la partie réelle de tous ses pôles est négative c-à-d que
pour tout pôle
Exemples
Les figures suivantes présentent les diagrammes des pôles et des zéros de deux systèmes, ainsi que leur réponse indicielle (avec
Système Stable
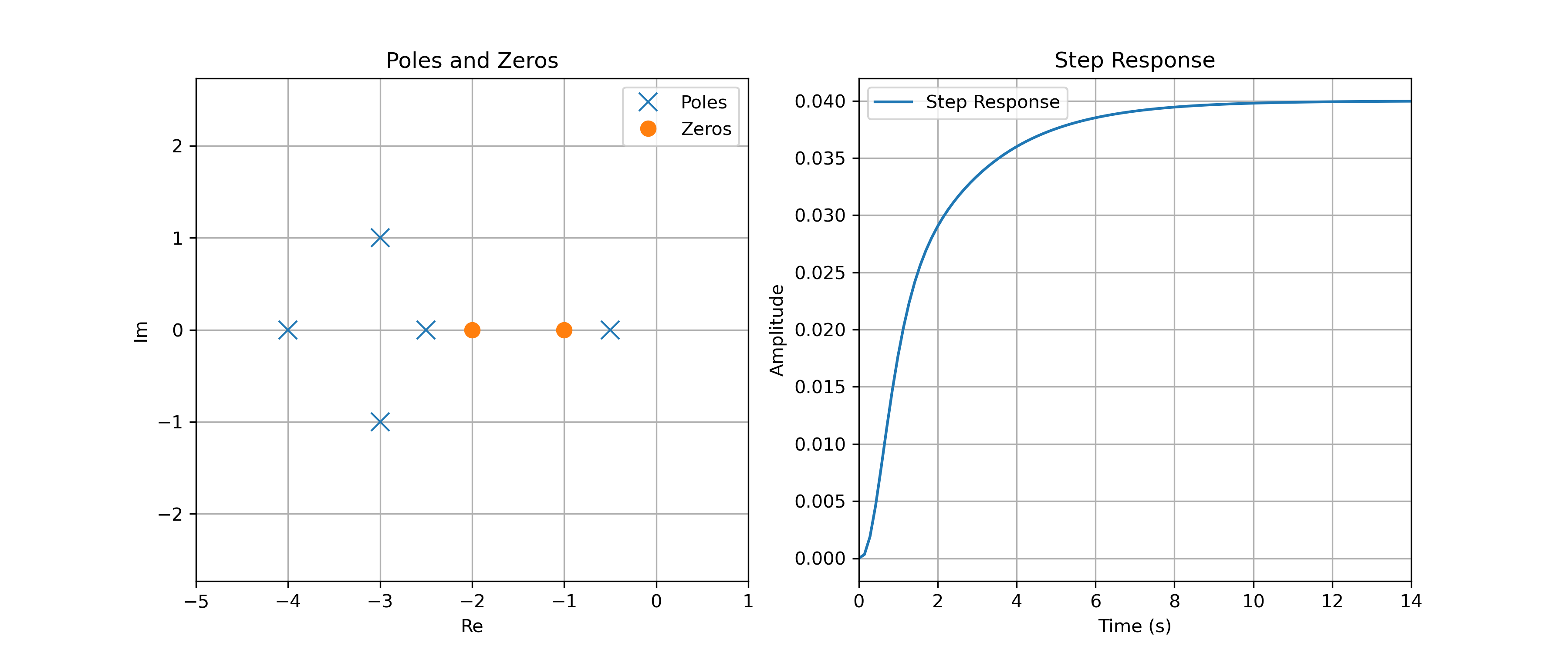
Dans la première figure, l'ensemble des pôles est situé sur le demi-plan gauche, c-à-d que tous les pôles ont une partie réelle négative. L'allure de la réponse indicielle permet de confirmer que le système est bien stable.
Système Instable
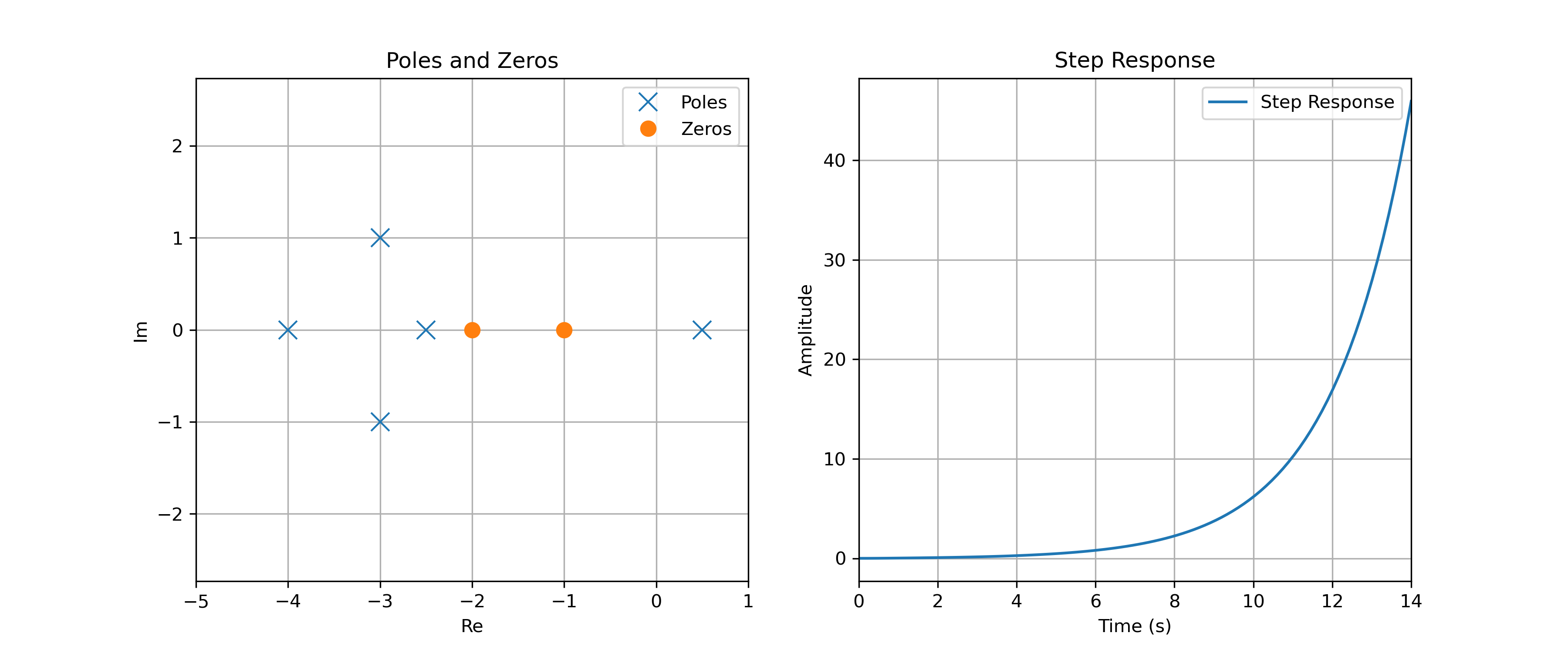
Dans la seconde figure, un pôle possède une partie réelle positive (
Cas de la Boucle fermée
Pour analyser la stabilité du système en boucle fermée
Lieux de Black et critère du revers
Le diagramme de Black-Nichols du système en boucle ouverte
Critère du revers
Pour qu’un système à retour unitaire soit stable en boucle fermée, le lieu de Black du système en boucle ouverte
Exemples
Les figures suivantes présentent les lieux de Black de deux systèmes de 3ieme ordre, ainsi que leur réponse indicielle en boucle fermée (avec
Système stable en boucle fermée
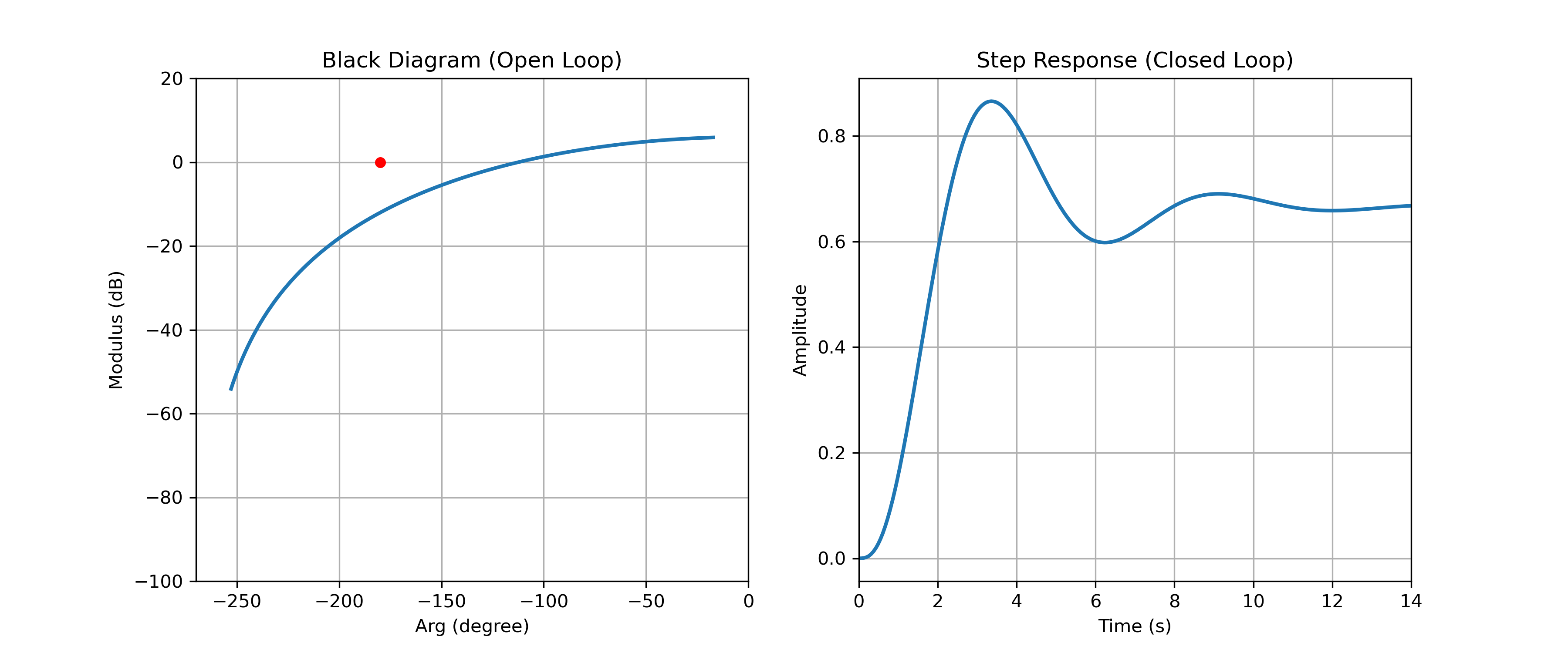
La figure ci-dessus présente le lieu de Black d'un système en boucle ouverte
Système instable en boucle fermée
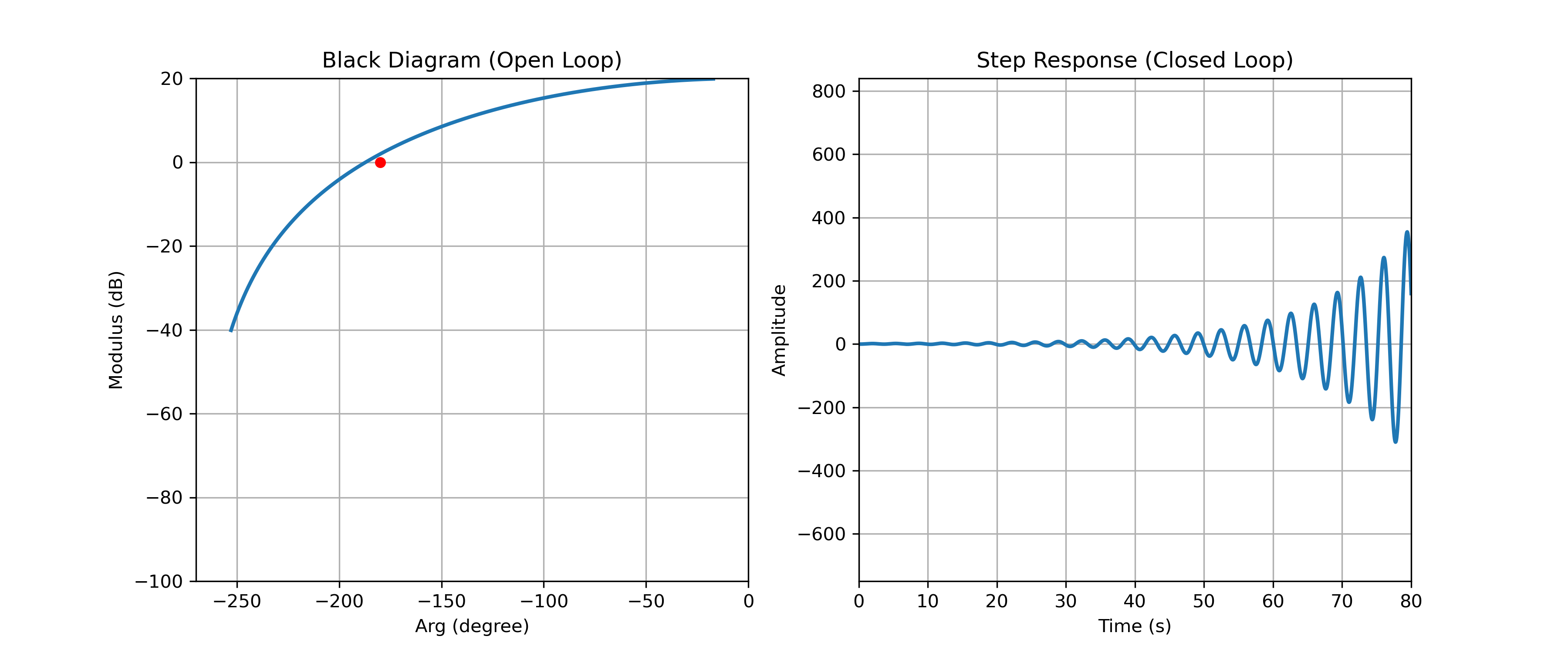
La figure ci-dessus présente le lieu de Black d'un système en boucle ouverte
Marges de Gain et de Phase
Le critère de stabilité est un critère dur: le système est soit stable, soit instable. En pratique, il est souvent préférable de recourir à des critères numérique pour caractériser la stabilité "relative" d'un système en boucle fermée. Dans ce contexte, deux critères sont couramment utiliser :
- Marge de Phase
: Distance en degrée par rapport au point critique lorsque . - Marge de Gain
: Distance en dB par rapport au point critique lorsque .
Lorsqu'un système est stable en boucle fermée, ces deux marges sont positives.
Exemple
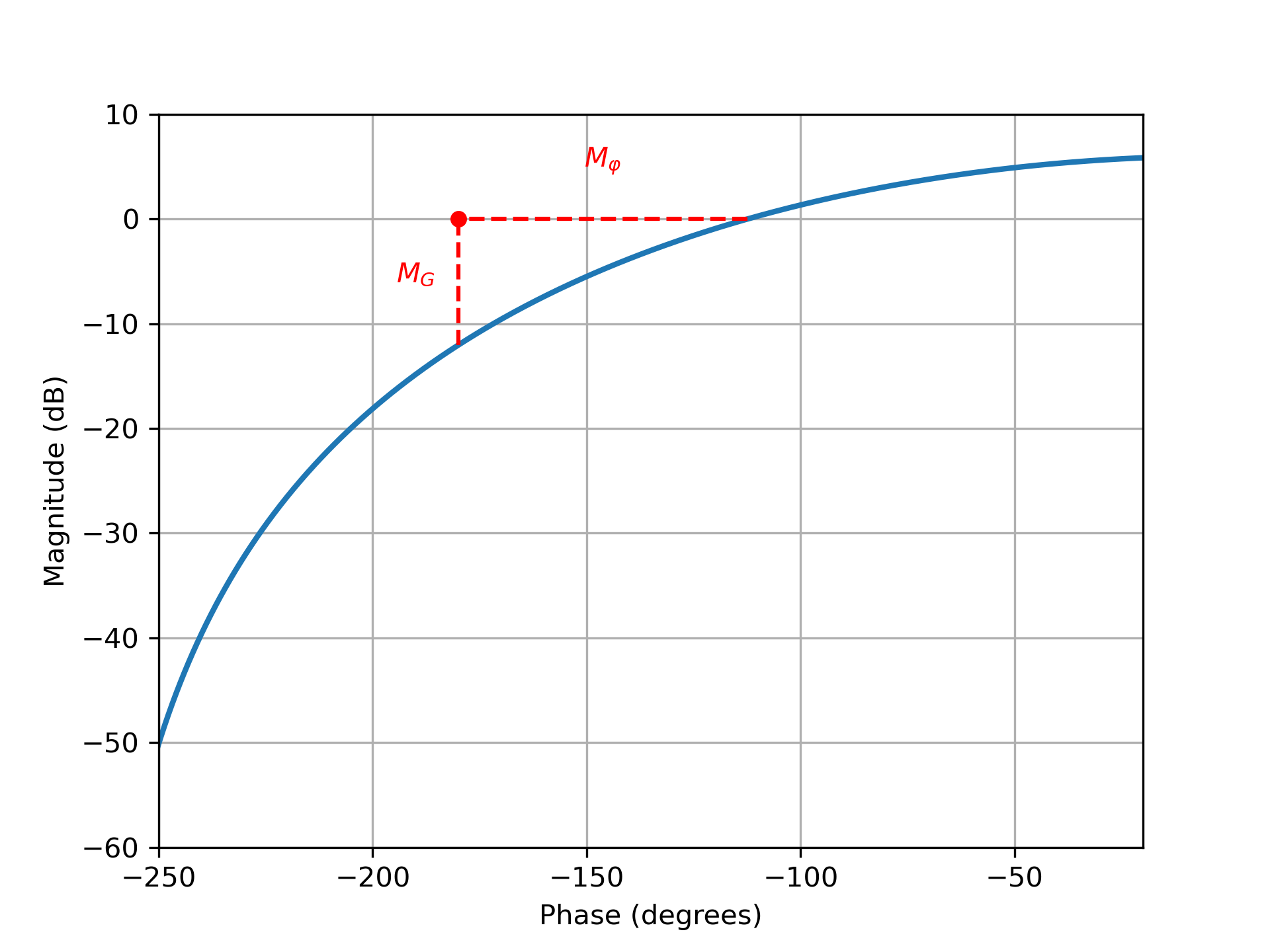
A titre d'exemple, la figure ci-dessus présente le lieu de Black d'un système de 3ieme ordre. Ce système est stable en boucle fermée. Concernant les marges, nous obtenons une marge de Gain
Correction et Apport de Phase
Pour gagner en stabilité en boucle fermée, un stratégie de correction possible consiste à "apporter" de la phase en boucle ouverte (translation du lieu de Black vers la droite).
